Úskalí moderního pojmu čísla

Základy moderní matematiky jsou spojeny s transformací pojmu čísla, ke které došlo na počátku novověku, a která dala vzniknout tomu, co nazýváme „čísla reálná“. Tuto zásadní změnu lze ilustrovat na jednoduchém příkladu odmocniny ze dvou. Dostaneme se při tom k překvapivému zjištění, že moderní matematika bez okolků pracuje s nečíselnými poměry, jako by to byla čísla.

Pro úspěchy moderní přírodní vědy a z ní vycházející technické civilizace je klíčová matematizace fyziky. Ta zahrnuje infinitezimální počet (obsahující integrály a derivace) a v případě kvantové teorie i komplexní čísla, což jsou nástroje přesahující chápání většiny neodborníků. Použitý termín „číslo“ nicméně spadá do všeobecné vzdělanosti a může vzniknout dojem, že tzv. „reálná čísla“ jsou dobře známá a neproblematická, a že tedy obtížnost moderní matematiky spočívá pouze v příliš komplikovaných výpočtech, v integrálech a derivacích, případně právě v zavedení čísel komplexních.

Základy moderní matematiky jsou nicméně spojeny s transformací samotného pojmu čísla, ke které došlo v 16. a 17. století, a která dala „reálným číslům“ vzniknout. Tato transformace umožnila vznik fyzikálních „veličin“, a tím kvantifikaci přírodních jevů, jež je jádrem matematické fyziky. Samozřejmost, se kterou pojem reálných čísel přijímáme, ztěžuje porozumění radikálnosti uvedené změny, a tím i porozumění myšlenkovému rámci, ve kterém se celá moderní přírodověda pohybuje. Pro stromy nevidíme les, což platí často i pro odborníky.

Antická matematika

Zmíněná zaslepenost se dobře ukazuje na moderním přístupu k antické matematice, který zcela dominoval historii matematiky nejméně do poloviny dvacátého století. Antická díla byla, a dodnes často jsou, přepisována do moderní notace s tichým předpokladem, že takto to jistě antičtí autoři jako Eukleidés nebo Diofantos mysleli, jen to nedovedli správným způsobem zformulovat. To je ovšem u takových myslitelů dost překvapivé, protože jde o zápis, který se dnes učí děti na základních školách. Je většina dnešních dětí srovnatelnými nebo dokonce lepšími matematiky, než byl třeba Diofantos?

Nelze popřít, že moderní přístup je po technické stránce opravdu nesrovnatelně efektivnější. Pokročilejší matematické partie by bez něj nebyly myslitelné. Nereflektovaný přístup založený na postupech zvládnutých na základní škole „pouze“ zakrývá pohled na skutečnou povahu moderní matematiky, která se od matematiky antické v podstatných ohledech liší, přestože z ní vychází.

Je to jeden z případů, kdy používáme výdobytky moderní techniky, aniž bychom rozuměli jejím nejhlubším myšlenkovým předpokladům. To měl na mysli Edmund Husserl, když psal o krizi evropské vědy, a na to reagoval Jan Patočka jednou ze svých „kacířských esejí“ nadepsanou „Je technická civilizace úpadková, a proč?“

Transformace pojmu číslo

Izák Newton je jedním z těch, kdo si byli moderní transformace pojmu čísla dobře vědomi. V úvodu své Arithmetica Universalis (poznámek z přednášek, jejichž vydání ovšem odmítl autorizovat) říká:

“Číslem nerozumíme ani tak nějakou mnohost jednotek, jako spíše abstraktní poměr mezi nějakou veličinou a jinou veličinou téhož druhu, kterou bereme za jednotku.“

Číslo ve svém původním významu odpovídá na otázku „kolik“, která vždy předpokládá, že víme kolik čeho, tedy co je jednotkou počítání. Pokud to jasné není, je třeba jednotku upřesnit či zvolit. Uvažme např. otázku „kolik smetany“, na kterou můžeme odpovědět různě, třeba „čtvrt litru“ (v obchodě) nebo „jednu lžičku“ (u kávy).

Jak je tomu, řekneme-li, že délka úhlopříčky jednotkového čtverce je odmocnina ze dvou? V tomto případě neodpovídáme na otázku „kolik“, ale na otázku „jak dlouhá“. Ve smyslu Newtonova citátu tedy mluvíme o poměru mezi úhlopříčkou a stranou čtverce. Proč tomu ale říkáme číslo? Je v naší otázce nějak přítomno původní „kolik“?

Průměr kruhu o jednotkovém poloměru je dva. To dává dobrý smysl v původním významu čísla: průměr je roven dvěma poloměrům, skládá se z nich. Podobně přímočarý je vztah mezi plochou čtverce s danou stranou a plochou čtverce nad jeho úhlopříčkou. Plocha většího čtverce je právě dvakrát plocha čtverce menšího, jak snadno vidíme z následujícího obrázku, když zvolíme za jednotku označený pravoúhlý trojúhelník. Menší čtverec má plochu dva tyto trojúhelníky, zatímco větší čtyři.

Pro závěr, že plochy čtverců jsou v poměru dvě ku jedné, pak můžeme argumentovat, že to je stejný poměr jako poměr čtyři ku dvěma. Vidíme, že i u čísel se může uplatnit Newtonova myšlenka poměru mezi kvantitami. Ani přirozené číslo nemusíme chápat pouze jako počet jednotek v daném množství, ale také jako poměr daného počtu k jednotce. Tento poměr je abstrahován ze vztahů mezi různými jinými počty. Abstrakcí zde rozumíme prostě to, že poměr 2:1 je tentýž jako poměr 4:2 či 6:3. Jedná se o stejný postup jako když říkáme, že buk je stromem stejně jako dub nebo bříza. (Nebo jako když jsme právě řekli, že oba postupy jsou stejné a označili jsme je jako „abstrakci“.)

Staré dobré měření a jeho meze

Otázkou zůstává, jaký je mezi oběma pohledy na číslo (počet a poměr) vztah. Viděli jsme, že odmocninu ze dvou jako poměr mezi stranou a úhlopříčkou je možné redukovat na počet prostřednictvím ploch čtverců nad těmito úsečkami. Takový výklad by byl neproblematický i pro Eukleida. Moderní chápání je ale jiné: odmocnina ze dvou je pro většinu z nás číslem prostě proto, že na kalkulačce se po jejím zadání objeví něco jako 1,4142135. Ať už je počet desetinných míst naší kalkulačky jakýkoli, víme, že se jedná o pouhou aproximaci. To znamená, že zvolíme za jednotku např. setinu strany a zjistíme, že úhlopříčka je delší než 141 a kratší než 142 takových setin.

To je dobře známý postup zvaný měření. Vezmeme si pravítko kalibrované na setiny uvažované jednotky, přiložíme ho k úhlopříčce a spočítáme čárky. Jednotka je, pokud možno, rovna nějakému domluvenému vzoru, který je vystaven za vraty Novoměstské radnice (český loket Přemysla Otakara II.) nebo uložen v Národním archivu v Paříži (původní definice metru jako jednotky SI).

Ani to by pro Eukleida nebyla žádná novinka, jen by to oprávněně nepovažoval za matematický (tedy v jeho chápání aritmetický či geometrický) postup v pravém slova smyslu, ale spíše za příklad starého známého praktického zeměměřičství, které právě Řekové svou geometrií zdokonalili a překonali. Eukleidés by tedy takto prezentovanou moderní matematiku rozhodně nepovažoval za krok vpřed. Sám by navíc uměl navrhnout následující vylepšení samotného aproximačního postupu měření, kterému říkal anthyphairésis (a který odpovídá tomu, čemu dnes říkáme „rozvoj do řetězového zlomku“).

Základní myšlenkou je volba správných jednotek. Volit za jednotky desetiny, setiny atd. je totiž zbrklé a nakonec nevýhodné. Pokud např. zvolíme dvanáctiny, zjistíme, že odmocnina ze dvou je zhruba 17/12, s téměř poloviční chybou než aproximace 1,41 používající setiny. (Ještě dramatičtější je situace u čísla π, tedy u poměru délky kružnice a jejího průměru, který lze aproximovat jako 355/113 s chybou, která je víc než dvakrát menší než aproximace 3,141592 používající miliontiny.)

Eukleidés tedy navrhuje postupovat následovně. Počátkem měření je srovnání úhlopříčky a samotné strany. Snadno nahlédneme, že úhlopříčka je delší než strana, ale kratší než dvě strany, její délka je tedy jedna strana a „kousek“, říkejme tomuto kousku zbytek. Otázka nyní je, jak velký tento zbytek v porovnání se stranou je. Je to polovina strany? Pak by úhlopříčka byla jeden a půl strany, tedy tři poloviny strany. Jednotkou by byla polovina strany a poměr by byl tři ku dvěma. Nebo je snad zbytek třetina strany? Pak by vhodnou jednotkou byla třetina strany a délka úhlopříčky by byla čtyři tyto třetiny.

Všimněme si, že vlastně hledáme poměr, který převráceně odpovídá otázce, kolik zbytků je strana: pokud by byla např. strana tři zbytky, byl by zbytek jedna třetina strany apod. Měříme tedy nyní stranu v jednotce, kterou je zbytek. Zatímco celkově nás zajímá poměr mezi úhlopříčkou a délkou, nyní nás jako pomocná otázka zajímá poměr mezi stranou a zbytkem. Pomocí kružítka (nebo pomocí milimetrového pravítka) je snadné ověřit, že zbytek se do strany vejde dvakrát, ale ne třikrát. Zbytek je tedy více než třetina a méně než polovina strany a úhlopříčka je více než čtyři třetiny strany a méně než jeden a půl strany.

Takto bychom mohli postupovat dál. Je ovšem jasné, že se velmi brzy dostaneme do situace, že úsečka, kterou měříme, a jednotka, pomocí níž měříme, budou příliš malé na to, aby bylo příslušné měření spolehlivé. Narážíme na meze praktického zeměměřičství, a je tedy sporné, zda je navržený postup opravdu výhodnější.

V případě úhlopříčky je však nyní možné si povšimnout pozoruhodného faktu, který je vidět na následujícím obrázku.

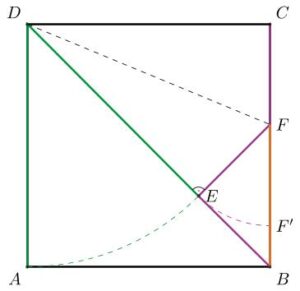
Náš zbytek je úsečka EB, která vznikla odebráním jedné strany z úhlopříčky. Veďme nyní kolmici z bodu E na stranu BC. Vzniklý trojúhelník BFE je polovinou čtverce, jehož stranou je náš zbytek a úsečka BF je jeho úhlopříčkou. Pointou celé konstrukce je pozorování, že i úsečka FC má délku zbytku neboli že úsečky BE, EF a FC se rovnají. To je vidět z toho, že trojúhelníky DFC a DFE jsou shodné, jsou to totiž pravoúhlé trojúhelníky se společnou přeponou DF a odvěsnami DC, resp. DE o délce strany původního čtverce. Z toho konečně plyne, že strana BC má délku jednoho zbytku a délky úhlopříčky čtverce jehož stranou je zbytek. Při měření strany BC zbytkem EB tedy nejprve odměříme jeden zbytek CF a pak stojíme před úkolem změřit úhlopříčku čtverce jeho stranou EB. To je ale původní úkol, zacyklili jsme se!

Strana i úhlopříčka jsou menší než na začátku, ale jejich poměr je stejný. To je základní geometrická intuice jevu nazývaného podobnost. Když nějaký obrázek zmenšíme, je to stále „stejný“ obrázek, jen menší. Všechny poměry zůstaly zachovány. Z uvedeného zjištění vyplývá, že výsledky dalšího měření známe do libovolné hloubky, aniž bychom museli dále měřit. Zbytek EB se do své úhlopříčky BF vejde jednou s „menším zbytkem“ F’B, který je k EB ve stejném poměru jako EB ke straně AB, a tak dále až donekonečna.

Dobrá a špatná zpráva

Poučení plynoucí z výše uvedené úvahy lze chápat jako dobrou i jako špatnou zprávu, přičemž hodnocení závisí na tom, o co nám při měření šlo, a také na vztahu k nekonečnu, které se objevilo na konci předchozího odstavce. Vztah k nekonečnu se přitom mezi antickou a moderní matematikou proměnil snad ještě více než pojem čísla.

Dobrá zpráva je, že můžeme snadno získávat stále lepší a lepší aproximace hledaného poměru pomocí zlomků. Pokud např. zanedbáme F‘B a budeme tvrdit, že strana BC je dvojnásobkem zbytku EB, dostaneme, jak jsme už jednou poznamenali, aproximaci úhlopříčky jako tří polovin strany. Tento odhad ale nyní můžeme použít na zpřesnění vztahu mezi EB a BF. Je-li BF tři poloviny EB, je strana CB pět polovin EB a úhlopříčka DB sedm polovin EB. Odhad poměru mezi stranou a úhlopříčkou čtverce tedy můžeme zpřesnit na pět ku sedmi. To znamená, že BF je zhruba sedm pětin EB, strana CB je zhruba dvanáct pětin a úhlopříčka DB zhruba sedmnáct pětin EB. Jednotka „pětina zbytku“ tedy dává odhad poměru mezi stranou a úhlopříčkou dvanáct ku sedmnácti, což je přesnější než 141 setin, jak jsme upozornili výše.

Špatná zpráva je, že proces nikdy neskončí, z čehož plyne, že poměr mezi stranou a úhlopříčkou čtverce se nedá přesně vyjádřit žádnou jednotkou. Délky jsou nesouměřitelné. To ale pro všechny antické matematiky znamená jediné: odmocnina ze dvou není číslo. Osud moderní matematiky závisí na schopnosti vysvětlit, jak je možné pracovat s objekty, které nejsou čísly, jako by čísly byly.

Štěpán Holub

Autor přednáší na matematicko-fyzikální fakultě Univerzity Karlovy v Praze.

Doporučená literatura:
Euclid, Elements, volně přístupné zde
Edmund Husserl, Krize evropských věd a transcendentální fenomenologie, Academia, 1996
Jakob Klein, Greek Mathematical Thought and the Origin of Algebra, Dover Publications, 1992
Jan Patočka, Kacířské eseje o filosofii dějin, Academia, 1990
Zbyněk Šír, Řecké matematické texty, Oikoymenh, 2011